What's going on at Black Mesa

The original Half-Life had rather low resolution whiteboards, making it difficult to fit much legible text on it. All the whiteboards at Black Mesa were the same texture

With the same formulas, which were mostly easily recognizable equations, such as $E = mc^2$ and the Newtonian gravity

For the fanmade recreation of Half-Life 1 in the Source engine, Black Mesa, the whiteboards were spruced up by making them higher resolution, with relevant content and unique for each room, although still fairly unrealistic in how well-written and small the text is on a laboratory whiteboard. A good compilation of all the whiteboards is available here. I'll look into the content of the theoretical physics-related ones, as I'm not particularly good with chemistry, crystallography or alien biology.

The first few whiteboards are about wormholes and faster-than-light travel, as befits Black Mesa's research on teleportation (although they appear in Sector C, which is more material science, not in Sector F, the Lambda Complex, where the actual teleportation research happens). The first one is on wormholes :

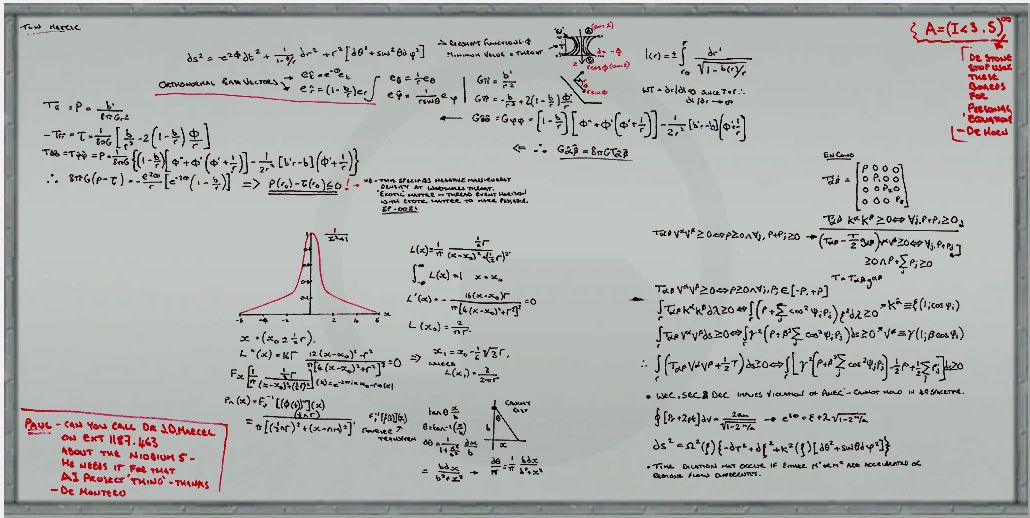
Let's break this down a bit. The first important line is this

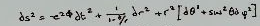
This is the metric tensor of the Morris-Thorne wormhole, expressed in the Schwarzdchild coordinates. From then on, the rest of the whiteboard roughly follows the same procedure as Morris and Thorne's original paper, Wormholes in spacetime and their use for interstellar travel: A tool for teaching general relativity. To the right are the properties of the functions making up the metric tensor.

Defining $\Phi$ as the redshift function, and putting the throat of the wormhole as the minimum value [of the shape function $b(r)$]. A drawing of the embedding of the surface defined by $(t= \text{const}, r, \theta = \pi/2, \varphi)$ is done, embedded in the three-dimensional space with cylindrical coordinates $(r, \varphi, z)$.

The proper radial distance $l$ is then defined with

It's a bit hard to make out exactly what they ask but from context it seems to be the usual requirement that $dr/dl = 0$ at the throat, or equivalently $dl/dr \to \infty$ [this implies that at the throat ($r = r_0$), we have $b(r_0) = r_0$].

Once the metric is dealt with, they define a tetrad (a set of orthonormal basis vectors)

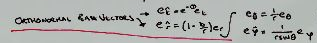
Then they compute the Einstein tensor along that tetrad

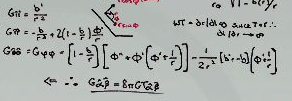
And from there, using the Einstein field equations $G_{\hat{\alpha}\hat{\beta}} = 8\pi G T_{\hat{\alpha}\hat{\beta}}$, they compute the stress-energy tensor, and associated to it, the energy density $\rho$, the radial tension $\tau$ and the tangential pressure $p$.

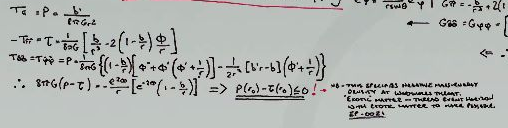
They then compute the quantity $\rho - \tau$, which is the product of the stress-energy tensor with a null curve of tangent $k^{\hat{\mu}} = (1, 1, 0, 0)$ in the tetrad basis, that is

$ 8 \pi G(\rho - \tau)$ corresponding to the Einstein tensor $G_{\hat{\alpha}\hat{\beta}} k^{\hat{\alpha}} k^{\hat{\beta}}$. This quantity is then found to be equal to

Since $b(r)$ has a minima at the throat of the wormhole ($r = r_0$) where $b(r_0) = r_0$, and any point beyond the throat will have $b(r) < r$, this leads to

Meaning that there is at least one point superior to $r_0$ where the derivative is positive, in particular this will be true at the throat itself, hence

which means that the throat requires exotic matter, as the comment indicates. The details of why this is so is in the following section

This starts first with writing the stress-energy tensor in matrix form. Since the metric leads to a Type I stress energy tensor, it is of the form

Then the Null Energy Condition (or NEC) is written down. The NEC states that given any null vector, the product of the stress-energy tensor with those vectors is positive or null,

For Type I stress-energy tensors, this will correspond to the following condition

that is, the sum of the energy density and momentum density in any direction is positive or zero, which is precisely the condition violated by the metric, for the radial momentum. The next equations concern other energy conditions, starting with the Weak Energy Condition (or WEC), which states that for any timelike vector $V$, we have

meaning that, for a Type 1 stress-energy tensor, we get

The energy density is positive or zero, as well as its sum with the momentum density in any direction, which is also rewritten as $p_i \in [-\rho, \rho]$ later.

Then there is the Strong Energy Condition (or SEC)

with $T = T_{\alpha \beta} g^{\alpha \beta}$, which can once again be rewritten as

The next three lines are the averaged versions of those energy conditions, the averaged null energy condition (ANEC), averaged weak energy condition (AWEC) and averaged strong energy condition (ASEC). For any curve $\gamma$ with tangent vector $k$ or $V$,

For a tangent vector $k^\alpha = \xi (1; \cos \psi_i)$ and $V^\alpha = \gamma (1; \beta \cos \varphi_i)$, this gives the relations \begin{eqnarray} \int (\rho + \sum_j \cos^2 \psi_j p_j) \xi^2 d\lambda &\geq& 0\\ \int (\rho + \beta^2 \sum_j \cos^2 \varphi_j p_j) \gamma^2 &\geq& 0\\ \int \left[ \gamma^2 (\rho + \beta^2 \sum_j \cos^2 \varphi_j p_j) \frac{1}{2} \rho + \frac{1}{2} \sum_j p_j \right] d\tau&\geq& 0 \end{eqnarray}

The follow-up isn't too clear, outside of the bit of text saying that violation of the WEC, SEC and DEC implies a violation of the ANEC (which is true).

Another whiteboard contains a few different things concerning faster-than-light travel.

First there is this metric tensor

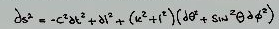
This is actually the same metric as previously, except that it is in the proper distance coordinate system, using the relation $l(r)$ seen above, giving the metric $$ds^2 = -c^2 dt^2 + dl^2 + r^2(l) (d\theta^2 + \sin^2 \theta d\varphi^2)$$

with the radius function $r = \sqrt{l^2 + k^2}$, corresponding to the Ellis-Bronnikov wormhole.

The diagram

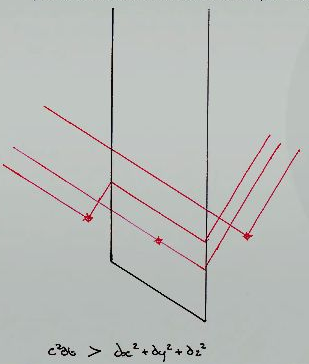
isn't actually the corresponding spacetime, but it is the diagram of the Kranikov tube, showing the light cones at various points, $c^2 dt^2 > dx^2 + dy^2 + dz^2$ simply indicating timelike curves.

The final part of the whiteboard concerns the Casimir effect

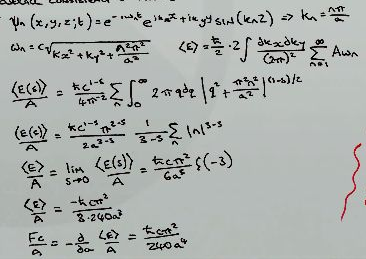
While realistically not ideal for propping up wormholes or Krasnikov tubes, the Casimir effect is a simple example of violation of most energy conditions, which wormholes do require. It's a fairly standard treatment (once again seemingly taken from the wikipedia article on the topic), first defining the eigenfunctions of a scalar field between two conducting plates separated by a length $a$ along the $z$ axis

with the momentum in the $z$ direction quantized as $k_n = \pi n / a$, and correspondingly the dispersion relation for the frequency

The expectation value of the energy of that field being

If we define $q^2 = k_x^2 + k_y^2$ and switch to polar coordinates, the integral becomes

or

This quantity is fairly divergent, just being an integral of an unbounded positive function over $\mathbb R$, as well as an infinite sum of a strictly increasing function, so we need to perform a regularization, in this case with the use of a zeta regulator. Instead of summing the quantity $\omega_n$, we'll sum $\omega_n |\omega_n|^{-s}$, with the limit $s \to 0$. This gives the appropriate forumla

with the integral evaluating to

Which is obviously divergent for $s = 0$. This corresponds to the limit of $s \to 0$ of the Riemann zeta function $\zeta(s - 3)$. While the Riemann zeta function isn't well-defined around that point, it is possible to analytically continue it in that region. We can then obtain

And the analytical continuation of $\zeta$ gives

For a total energy of

It is followed by a simple calculation of the Casimir force generated by moving the plates,

The following whiteboard is a calculation of evaporation time for Schwarzschild black holes via Hawking radiation (the derivation of which is possibly taken from the wikipedia article on the topic) :

Consider a black hole of mass $M$, corresponding to a total energy of $E = Mc^2$. The total power radiated will be equal to the change in its energy

The power radiated $P$ is known from the Hawking derivation of the radiation

of which we will split out the mass to obtain

Then we can simply solve the evaporation time as a simple ordinary differential equation of the mass, via

meaning that the energy radiated away is lost to the total mass. Using the common physicist trick of treating differentials as real objects, we get

The black hole starts at time $t = 0$ at mass $M = M_0$ and finishes at time $t = t_{ev}$ at mass $M = 0$, with the solution

which gives us the evaporation time as

The rest of the calculations are just the evaporation times for two masses : the Planck mass and one solar mass. For the Planck mass

the corresponding evaporation time is

while for one solar mass,

The formulas are then expressed in SI units

While the first part is some sort of mix of chemical and alchemical notation, the second is related to radioactive decay. The diagram is the Feynman diagram of a beta netative ($\beta^-$) decay, as seen from the perspective of quantum chromodynamics

with a neutron (composed of three quarks $udd$) emitting a $W^-$ boson, via the process $d \to u + W^-$, turning it into a proton ($uud$). The $W^-$ boson then decays into an electron and anti-electronic neutrino, $W^- \to e^- + \bar \nu_e$.

The text itself is a standard derivation of the eponymous half life formula for radioactive decay. First they define the half-life in terms of the decay constant