1. Articles
2. CS
3. Lazy Bird : A purely functional language

Lazy Bird : A purely functional language

---

Logical combinators are one of the oldest form of Turing complete system, going back all the way to Schönfinkel's 1924 paper "On the building blocks of mathematical logic", preceding both Church's lambda calculus and Turing's machine (as well as the older version of such a machine, the Post machine), though their status as such a system wasn't known at the time.

Not many languages have implemented them directly, as they are not particularly useful for actual programming, but a few esoteric languages have done it, most famously Unlambda

Lazy Bird is a small extension of Unlambda, along with the modification that it uses lazy evaluation (i.e. it evaluates the outermost function first when possible), rather than Unlambda's eager evaluation, which evaluates the innermost function first. The "bird" part of the name comes from the fact that the logical combinators used come from the most part from Smullyan's book "To Mock a Mockingbird", where all combinators are associated with birds.

Logical combinators

The basis of the language is made of logical combinators, which are pure functions, each of one arguments. As such, each function takes another function as an argument, and returns another funtion. These functions are called logical combinators.

(to avoid an overload of parenthesis, they will only be written when a letter isn't a direct argument of the previous letter, so that $(A(B)) (C)$ will be written as $A B C$)

The simplest logical combinator is the identity $I$, which, given another combinator $x$, returns $x$ :

$$I(x) = x$$

In terms of lambda calculus, it can be expressed as $\lambda x . x$.

The logical combinator $K$ does some currying and returns another function which will in turn return a constant made of the first argument. To make it more clear,

$$Kxy = x$$

$K(x)$ returns the constant function which will return $x$ for all inputs. In terms of lambda calculus, it is the expression $K = \lambda x.(\lambda y.x)$, which evaluated once gives us $\lambda y.x$.

The total list of combinators used are mostly from Unlambda and Smullyan's book

Symbol	Name	Action	Lambda expression
i	Identity	$Ix = x$	$\lambda x . x$
k		$Kxy= x$	$\lambda x. (\lambda y . x)$
s		$Sxyz= (x z (y z))$	$\lambda x . (\lambda y (\lambda z. x z (y z)))$
m	Mockingbird	$Mx = xx$	$\lambda x . xx$
0	Kite	$0xy = y$	$\lambda x . (\lambda y. y)$
w	Warbler	$Wxy = xyy$	$\lambda x . (\lambda y. xyy)$
u	Turing	$Uxy = y(xxy)$	$\lambda x . (\lambda y. y(xxy))$
o	Owl	$Oxy = y(xy)$	$\lambda x . (\lambda y. y(xy))$
t	Thrush	$Oxy = yx$	$\lambda x . (\lambda y. yx)$
l	Lark	$Oxy = x(yy)$	$\lambda x . (\lambda x(yy))$
b	Bluebird	$Bxyz = x(yz)$	$\lambda x . (\lambda y. (\lambda z. x(yz))$
c	Cardinal	$Cxyz = xzy$	$\lambda x . (\lambda y. (\lambda z. xzy))$
q	Queer	$Qxyz = y(xz)$	$\lambda x . (\lambda y. (\lambda z. y(xz) ))$
v	Vireo	$Vxyz = zxy$	$\lambda x . (\lambda y. (\lambda z. zxy ))$
@	-	$@x = xSK$	$\lambda x .xSK$
#	-	$\#x = \#$	$\lambda x. (\lambda y . (\lambda z. yy))(\lambda y' . (\lambda z'. y'y'))$

Syntax

As is the tradition in most combinator-based languages, since every function is a function of just one argument, we can forgo the use of parenthesis to use Polish notation with the use of a function application operator, denoted `. So that the operation $I(I)$ will be written as `ii Or the more complex function $(S((S(K))(K)))((S(K))(K))$ as ``s``skk``skk

Side-effects

As a purely functional language, there should be no side-effects involved, but it would not be particularly easy to use if that were the case. Following Unlambda's convention, the only side-effects will be a class of identity combinators with side-effects, the side effect being the printing of a character. Each of them being of the form .x, which has the same behaviour as i, except for the side effect of printing the character x when evaluated. The only exception is the newline character, represented by the combinator r.

A simple example is the classic Hello World :

For input, a simple method is to convert user input into Church numerals. For this we will use the combinator _, which when evaluated, will pause the execution of the program and await for keyboard input, which will then be converted into the appropriate Church numeral depending on its ASCII value.

Implementation

Unfortunately, most languages are ill-equipped to offer a simple implementation of logical combinators, as most languages are typed to some degree and will not allow to pass generic functions as arguments. In other words, we can't really implement this on most languages :

Though this may be possible to do in assembly, where both arguments and functions are just integers. It is still possible to write an interpreter of combinators in high-level languages. There are two main ways to do this, first as a string rewriting problem, or as a graph rewriting problem..

String rewriting

If we treat the program as a stringrewriting problem, the program is just defined by the input string, and every step of execution will rewrite this string. For instance, the most basic program which can actually be evaluated into a different string will be $I(I)$. This string

$$I(I) \to I$$

First we need to check if the input string is of the correct syntax. There are a few different conventions we can use, but we will mostly deal with three acceptable scenarios.

1. The string is empty, in which case the program leaves immediatly, as there are no combinators to evaluate.
2. The string is a single combinator, meaning either a single letter or one of the printing combinator of the form .x. There's two possible behaviours we can choose here : Either we consider that this operator cannot be evaluated as it has no arguments, or we can consider that a program (program) is really meant to be `(program)i, or some more complex setup (for instance an infinity of identity operators, or some input we decide from the command line). For simplicity I recommend simply notevaluating it.
3. The string starts with an application operator, and is of the form `(valid combinator expression)(valid combinator expression), where the valid combinator expression will be either a single combinator or itself another application of two valid expressions. The program will then try to evaluate the first combinator with the second as its argument.

Overall, the language has the following Backus-Naur form

< Combinator > ::= "S" | "K" | "I" | ...
< Expression > ::= < Combinator > | "`" < Expression > < Expression >
< Program > ::= "" | < Expression >

An important function for checking the syntax, and also useful later on, will be to split an expression into its two arguments. This can be done rather simply by counting the number of combinators and the number of application operators encountered in the string. The basic expression of two combinators `CC will have one more combinator than application operator. This pattern repeats itself for any arbitrary expression, as we will construct it recursively by removing one operator and replacing it by one application operator and two combinators, such as ``CCC, `C`CC, ``CC`CC, etc.

Once the syntax has been cleared, we can evaluate the expression without fear of troubles. To do this, we go through the string until we encounter a combinator, the behaviour will then depend on the combinator we first encounter. For our purpose, we will only have three main cases : the combinator encountered requires either one, two, or three arguments (in the currying sense), since the string transformation rules that we defined do not have any combinators requiring more than 3 arguments.

If we need $n$ arguments for the function, this means that the combinator needs to be preceded by $n$ function application operators, otherwise it cannot be evaluated. In this case, we will proceed onward in the string until we find another combinator.

Once we have an operator which can be evaluated, we get the appropriate number of arguments required. For instance, in the case of the $S$ combinator, we will require 3 arguments, which are obtained by first getting the expression following `s, then the expression following ``s(argument 1), and finally the expression following ```s(argument 1)(argument 2). With those three arguments, we then rewrite the string from

[...]```s(argument 1)(argument 2)(argument 3)[...]

to

[...]``(argument 1)(argument 3)`(argument 2)(argument 3)[...]

Graph rewriting

The issue of the string rewriting is that it is fairly heavy to calculate every step, especially every step involving a search for every argument. A more efficient way to treat it is to consider it as a binary tree, where every internal vertex corresponds to a function application operator, and every leaf corresponds to a combinator. Then the action of every combinator will be the transformation of a subtree, either 1, 2 or 3 vertex deeper than the operator considered. The expression `ix will then be represented by the binary tree

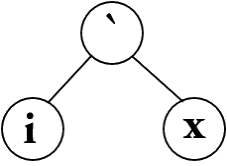
which will transform to

Conversion between lambda calculus and combinators

There is a fairly straightforward conversion of combinators into lambda calculus, as the table of combinators imply, but the other way around is a bit more complex. This is done through a process called abstraction elimination, by which any lambda expression without free variables can be converted to a logical combinator.

\begin{eqnarray} T[x] &\rightarrow& x \\ T[E_1 E_2] &\rightarrow& T[E_1] T[E_2] \\ T[\lambda x. E] &\rightarrow& K T[E] \\ T[\lambda x.x] &\rightarrow& I \\ T[\lambda x. \lambda y. E] &\rightarrow& T[\lambda x. T[\lambda y. E]] \\ T[\lambda x.E_1 E_2] &\rightarrow& S T[\lambda x.E_1] T[\lambda x.E_2] \end{eqnarray}

Programming with combinators

Church numerals

Logical combinators use the same basic scheme for handling integers, which is Church numerals, combinators of the form

$$Nxy = x(x(x(...x(y))))$$

Where the function $x$ is applied $N$ times to $y$. In terms of lambda calculus, this corresponds to

$$N = \lambda x. \lambda y. x(x(x(...x(y)...)))$$

And in particular, $0$ is represented by the $0$ combinator

$$0xy = y$$

The next few numbers can be represented by the following combinators : \begin{eqnarray} 1xy &=&Ixy = xy\\ 2xy &=& SBIxy = Bx(Ix)y = Bxxy = x(xy)\\ 3xy &=& SB(SBI)xy = Bx(SBIx)y = Bx(Bxx)y = x(Bxxy) = x(x(x(y))) \end{eqnarray}

Arithmetics

Lists

Similarly to LISP, lists are done using ordered pairs. That is, the list $(a,b,c,...)$ is actually the ordered pair

$$\langle a, \langle b, \langle c, .... \rangle \rangle \rangle$$

Ordered pairs are represented by the combinator $V$, so that

$$\langle x, y \rangle = Vxy$$ Or, in lambda expressions, $$Vxy = \lambda z. z x y$$

This means that applying this list to a function will apply the function to all elements of the list.

$$Vxyf = (f(x))(y)$$

The combinators for the first and last element of the pair (CAR and CDR in LISP) are represented by $TK$ and $T0$

$$TK(Vxy) = VxyK = Kxy = x$$ $$T0(Vxy) = Vxy0 = 0xy = y$$

Conditionals, loops and recursion

The simplest way to perform an infinite loop is via recursion with the Turing combinator

$$UUx = x(UUx) = x(x(UUx)) = x(x(x(UUx))) = ...$$

A few sample programs

---

Last updated : 2017-10-29 07:43:56